Graph Grammar

A Generative Theory of Tonal Music by Fred Lerdahl and Ray Jackendoff (MIT, 1983) proposes the effectiveness of a grammatical approach to analyzing music. This seems also like a very natural and simple way to generate music-like tone sequences. My goal was then to somehow combine this idea with thermodynamic simulation of a system near a critical point to produce fractal pitch fluctuations.

The problem is that grammars are usually thought of as a way to produce a string, i.e. a one-dimensional array. My whole thermodynamic approach is to envision the musical structure as a higher dimensional mesh or lattice. The performance of the piece is then a walk through that mesh. I have been predefining the meshes up to now as just very regular structures, which has produced rather monotonous music. So I looked for a way to allow richer structure - rhythmic and topological - to emerge from a set of rules, rather than just imposing the final structure from the start.

The key requirement is to generate a structure with interconnections that are more two dimensional (or higher) than one dimensional. It is a fundamental result in statistical mechanics, due to Peierls in the 1930's, than one dimensional systems cannot support a phase transition. Onsager then exhaustively demonstrated, in the 1940's, the character of the phase transition in the two dimensional Ising model. So somehow I need to generate a two (or more) dimensional structure.

While the precise statistical mechanical requirements are not altogether clear (at least to me!), a graph with only three edges per vertex is capable of representing structures of arbitrarily high dimensionality: given any arbitrary graph, just replace each vertex that originally has more than three edges with a loop of simpler vertices, one simpler vertex per original edge. These simpler vertices will thus have only three edges - two to connect up the loop, and one for the original edge.

So for a musical structure: how about arranging the notes in a big loop, and give each note one extra neighbor, in general temporally distant, along with the immediate temporal neighbors before and after the note. This kind of structure can easily be generated by a graph grammar. Such a grammar will take a note and its distant neighbor, and expand these into short sequences of notes, each with distant neighbor relations. Many such graph transformations can be defined. By applying these recursively, quite complex topological structures can be generated.

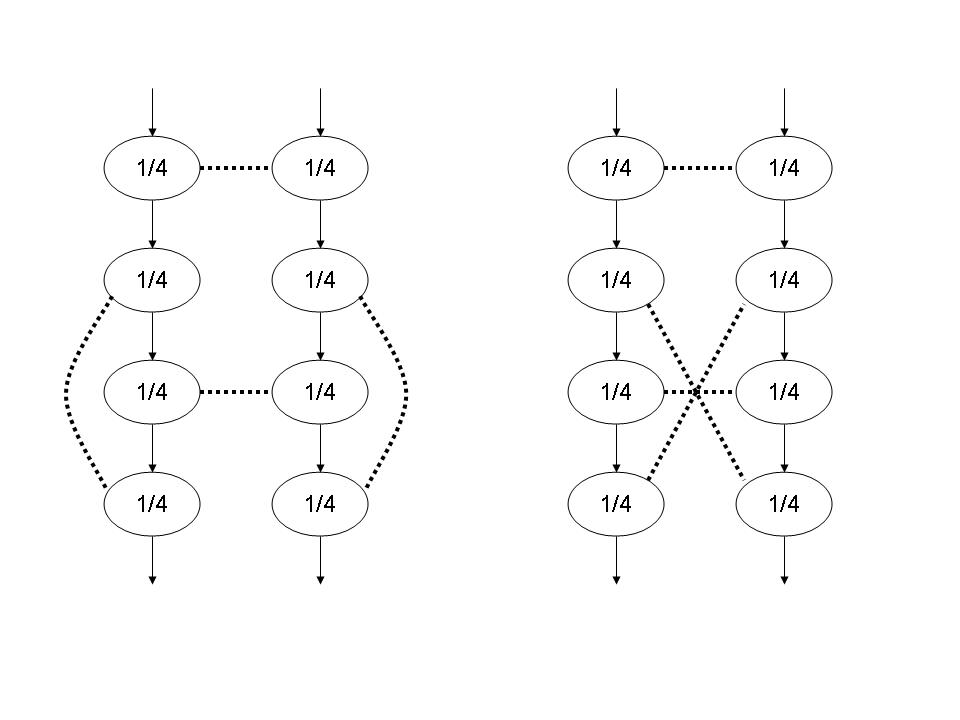
Here are a few simple such graph transformations. The number in the circle is the length of each note.

When these actions are applied recursively from a simple starting configuration, complex structures can be created:

A wide variety of transformations can be defined, such as:

When a thermodynamic simulation is performed on a system whose cost function is defined by such a graph, a phase transition is indeed observed - there is a sharp spike in the thermal capacity, and a sudden onset of long range order. Here is a plot of the thermal capacity as a function of the temperature, with the temperature on a logarithmic scale:

The onset of long range order can clearly be seen in the chart below. In this run there are 159 possible pitch values at each vertex, i.e. three octaves (this is microtonal music with 53 pitches per octave). In this chart, the three octaves have been folded together, so that each of the 2330 vertices in the graph is assigned one of the 53 pitch classes. If there were no long range order, each pitch class would occur on roughly 44 vertices on average, with some random variation about that average - typically +/- 6 or 7. In this chart, the 53 pitch classes are sorted, from those that occur on the smallest number of vertices, to those that occur on the most vertices. The blue bars show the frequencies of occurances of pitch classes a bit above the transition, at a temperature of 7.08. The pitch class that occurs least frequently occurs on 24 vertices, while the most frequent pitch class occurs on 74 vertices.

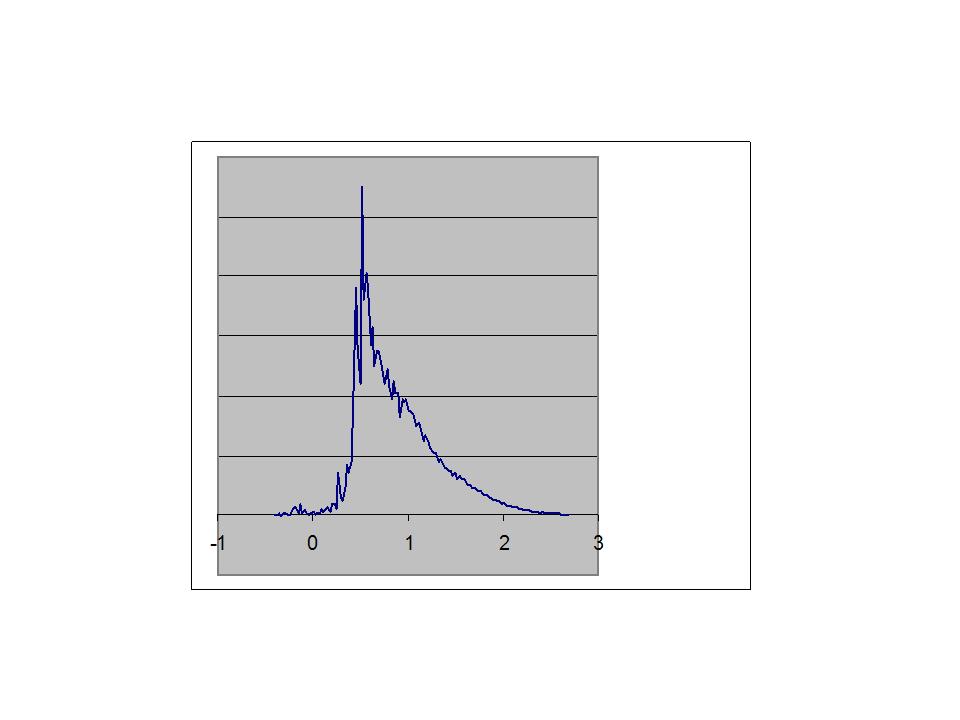
The yellow bars show the pitch class frequencies a bit below the transition, at a temperature of 3.12. Here, 15 pitch classes do not occur at all, while two pitch classes occur more than 200 times each. A small number of pitch classes is coming to dominate the entire graph.

The lowest cost solution, with all vertices containing exactly the same pitch, should be found at a sufficiently low temperature, given enough simulation time and a slow enough decrease in the temperature. This particular run froze up at a temperature of about 0.3, with 29 pitch classes not occurring at all and the most frequent pitch class occurring 407 times.

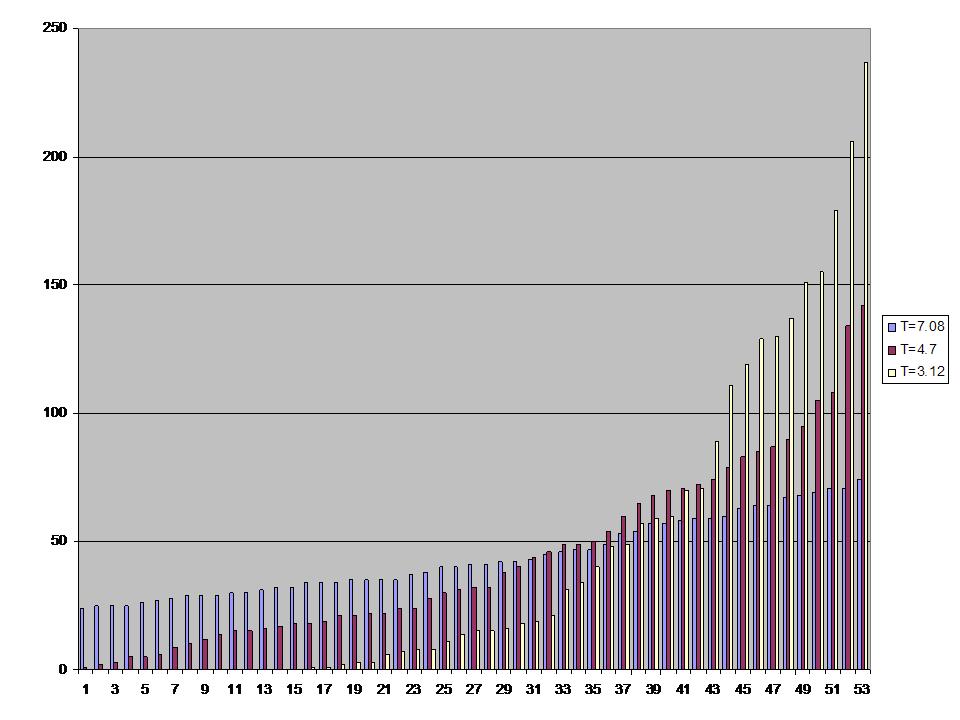
A snapshot of the note sequence can be taken near the transition - here is a 6 MB mp3 file. (This is a run very similar to the one from which the charts above were derived, but not identical.) Perhaps one will be able to hear in the result some of the structure that went into its creation?

This is another piece, with three parts of related structure.

Here is an explanation of the microtonality involved in this music.